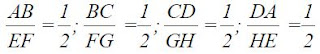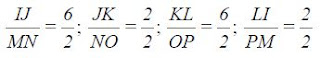Pengertian dan Contoh Soal Kesebangunan Bangun Datar
Agustus 22, 2016
Edit
Berikut ini adalah pembahasan tentang pengertian kesebangunan, syarat benda sebangun, kesebangunan bangun datar, contoh soal kesebangunan, contoh soal kesebangunan smp kelas 9, contoh soal segitiga sebangun, contoh soal kesebangunan segitiga, contoh soal kesebangunan bangun datar.
Pernahkah kamu memperhatikan papan catur? Setiap petak satuan pada papan catur, baik yang berwarna hitam maupun yang berwarna putih, memiliki bentuk dan ukuran yang sama.
Tahukah kamu, disebut apakah bangun-bangun yang sama bentuk dan ukurannya? Untuk menjawabnya, pelajarilah pembahasan ini dengan baik.
Bentuk benda pada foto mula-mula dengan foto yang telah diperbesar adalah sama, tetapi ukurannya berlainan dengan perbandingan yang sama. Gambar benda pada foto mula-mula dengan foto yang telah diperbesar merupakan contoh dua bangun yang sebangun.
Sekarang, coba kamu perhatikan Gambar di atas! Sebangunkah persegipanjan ABCD dengan persegipanjang EFGH? Pada persegipanjang ABCD dan persegipanjang EFGH, perbandingan panjangnya adalah 4 : 8 = 1 : 2.
Adapun perbandingan lebarnya adalah 2 : 4 = 1 : 2. Dengan demikian, perbandingan sisi-sisi yang bersesuaian pada kedua persegipanjang tersebut dapat dinyatakan sebagai berikut.
Kemudian, perhatikan sudut-sudut yang bersesuaian pada persegipanjang ABCD dan persegipanjang EFGH. Oleh karena keduanya berbentuk persegipanjang, setiap sudut besarnya 90° sehingga sudut-sudut yang bersesuaian pada kedua bangun tersebut sama besar.
Artinya kedua persegi panjang tersebut memiliki sisi-sisi yang bersesuaian dan sebanding sedangkan sudut-sudut yang bersesuaian sama besar. Oleh karena itu, persegipanjang ABCD dan persegipanjang EFGH dikatakan sebangun.
Jawab:
a. Perhatikan persegipanjang IJKL dan persegi MNOP.
(i) Perbandingan panjang sisi-sisi yang bersesuaian adalah
Jadi, sisi-sisi yang bersesuaian pada persegipanjang IJKL dan persegi MNOP tidak sebanding.
(ii) Besar setiap sudut pada persegipanjang dan persegi adalah 90° sehingga sudut-sudut yang bersesuaian pada persegipanjang IJKL dan persegi MNOP sama besar.
Dari (i) dan (ii) dapat disimpulkan bahwa persegipanjang IJKL dan persegi MNOP tidak sebangun.
b. Perhatikan persegi MNOP dan persegi QRST.
(i) Perbandingan panjang sisi-sisi yang bersesuaian adalah
Jadi, sisi-sisi yang bersesuaian pada persegi MNOP dan persegi QRST sebanding.
(ii) Oleh karena bangun MNOP dan QRST berbentuk persegi, besar setiap sudutnya 90° sehingga sudut-sudut yang bersesuaian pada kedua bangun tersebut sama besar.
Dari (i) dan (ii) dapat disimpulkan bahwa persegi MNOP dan persegi QRST sebangun.
c. Dari jawaban a telah diketahui bahwa persegipanjang IJKL tidak sebangun dengan persegi MNOP. Dengan demikian, persegipanjang IJKL juga tidak sebangun dengan persegi QRST.
Pernahkah kamu memperhatikan papan catur? Setiap petak satuan pada papan catur, baik yang berwarna hitam maupun yang berwarna putih, memiliki bentuk dan ukuran yang sama.
Tahukah kamu, disebut apakah bangun-bangun yang sama bentuk dan ukurannya? Untuk menjawabnya, pelajarilah pembahasan ini dengan baik.
Pengertian Kesebangunan Bangun Datar
Dalam kehidupan sehari-hari, pasti kamu pernah mendengar istilah memperbesar atau memperkecil foto. Ketika kamu memperbesar (atau memperkecil) foto, berubahkah bentuk gambarnya?Bentuk benda pada foto mula-mula dengan foto yang telah diperbesar adalah sama, tetapi ukurannya berlainan dengan perbandingan yang sama. Gambar benda pada foto mula-mula dengan foto yang telah diperbesar merupakan contoh dua bangun yang sebangun.
 |
| Gambar: Dua Persegi Panjang yang Sebangun |
Sekarang, coba kamu perhatikan Gambar di atas! Sebangunkah persegipanjan ABCD dengan persegipanjang EFGH? Pada persegipanjang ABCD dan persegipanjang EFGH, perbandingan panjangnya adalah 4 : 8 = 1 : 2.
Adapun perbandingan lebarnya adalah 2 : 4 = 1 : 2. Dengan demikian, perbandingan sisi-sisi yang bersesuaian pada kedua persegipanjang tersebut dapat dinyatakan sebagai berikut.
Kemudian, perhatikan sudut-sudut yang bersesuaian pada persegipanjang ABCD dan persegipanjang EFGH. Oleh karena keduanya berbentuk persegipanjang, setiap sudut besarnya 90° sehingga sudut-sudut yang bersesuaian pada kedua bangun tersebut sama besar.
Artinya kedua persegi panjang tersebut memiliki sisi-sisi yang bersesuaian dan sebanding sedangkan sudut-sudut yang bersesuaian sama besar. Oleh karena itu, persegipanjang ABCD dan persegipanjang EFGH dikatakan sebangun.
Kesebangunan adalah kesamaan perbandingan panjang sisi dan besar sudut antara dua buah bangun datar atau lebih.
Syarat Kesebangunan
Jadi, dua atau lebih bangun dikatakan sebangun jika memenuhi syarat-syarat sebagai berikut.- Panjang sisi-sisi yang bersesuaian pada bangun-bangun tersebut memiliki perbandingan yang senilai.
- Sudut-sudut yang bersesuaian pada bangun-bangun tersebut sama besar.
Contoh Soal Kesebangunan Bangun Datar
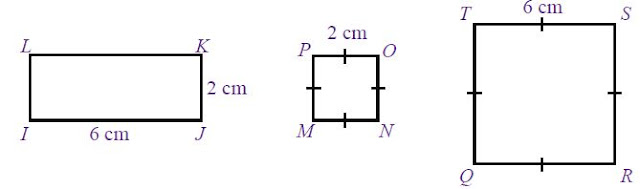
Di antara gambar-gambar berikut, manakah yang sebangun?Jawab:
a. Perhatikan persegipanjang IJKL dan persegi MNOP.
(i) Perbandingan panjang sisi-sisi yang bersesuaian adalah
Jadi, sisi-sisi yang bersesuaian pada persegipanjang IJKL dan persegi MNOP tidak sebanding.
(ii) Besar setiap sudut pada persegipanjang dan persegi adalah 90° sehingga sudut-sudut yang bersesuaian pada persegipanjang IJKL dan persegi MNOP sama besar.
Dari (i) dan (ii) dapat disimpulkan bahwa persegipanjang IJKL dan persegi MNOP tidak sebangun.
b. Perhatikan persegi MNOP dan persegi QRST.
(i) Perbandingan panjang sisi-sisi yang bersesuaian adalah
Jadi, sisi-sisi yang bersesuaian pada persegi MNOP dan persegi QRST sebanding.
(ii) Oleh karena bangun MNOP dan QRST berbentuk persegi, besar setiap sudutnya 90° sehingga sudut-sudut yang bersesuaian pada kedua bangun tersebut sama besar.
Dari (i) dan (ii) dapat disimpulkan bahwa persegi MNOP dan persegi QRST sebangun.
c. Dari jawaban a telah diketahui bahwa persegipanjang IJKL tidak sebangun dengan persegi MNOP. Dengan demikian, persegipanjang IJKL juga tidak sebangun dengan persegi QRST.