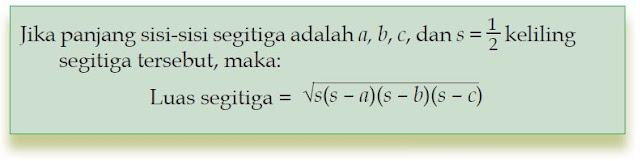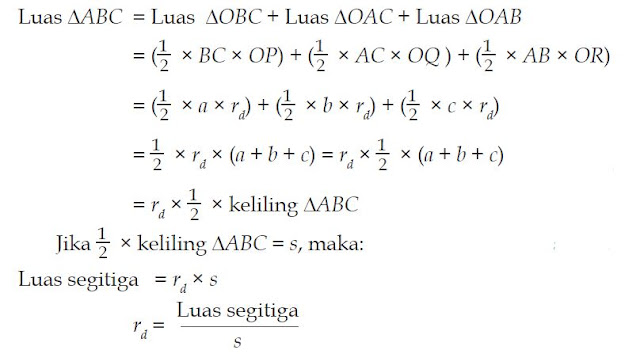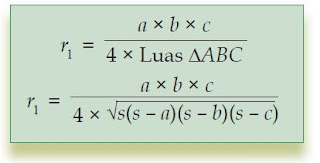Rumus Mencari Jari-jari Lingkaran Dalam Segitiga dan Lingkaran Luar Segitiga beserta Contoh Soalnya
Juli 31, 2016
Edit
Berikut ini adalah pembahasan tentang Panjang Jari-Jari Lingkaran Dalam Segitiga dan Lingkaran Luar Segitiga, rumus jari jari lingkaran luar segitiga, rumus jari jari lingkaran dalam segitiga, contoh soal jari jari lingkaran dalam segitiga, contoh soal jari jari lingkaran luar segitiga, rumus mencari jari jari lingkaran, rumus lingkaran dalam segitiga.
Sehingga, dapat kita simpulkan untuk sebarang segitiga dengan panjang sisi-sisinya a, b, dan c, serta s = ½ × keliling segitiga, maka jari-jari lingkaran dalam segitiga tersebut adalah:
Perhatikan ΔAQB dan ΔACP!
Besar ∠ABQ (sudut keliling yang menghadap busur AQ dan menghadap diameter lingkaran) = 90o = ∠APC (karena AP adalah garis tinggi ΔACP, maka AP⊥BC). Besar ∠AQB = ∠ACP karena sudut keliling menghadap busur yang sama). (Materi bahasan sudut keliling akan dibahas pada subbab berikutnya).
Karena terdapat dua buah sudut yang bersesuaian sama besar, maka ΔAQB dan ΔACP sebangun (bentuknya sama, tetapi ukurannya berbeda). Sehingga dapat ditulis secara matematis dalam bentuk berikut.
Sehingga, dapat kita simpulkan untuk sebarang segitiga dengan panjang sisi-sisinya a, b, dan c, serta s = ½ × keliling segitiga, maka jari-jari lingkaran luar segitiga adalah:
a. Keliling lingkaran dalam segitiga
b. Luas lingkaran luar segitiga
Penyelesaian:
Diketahui a = 6 cm, b = 8 cm, c = 10 cm
Rumus Mencari Jari-jari Lingkaran
Untuk mengetahui panjang jari-jari lingkaran dalam dan luar segitiga, kita harus mengetahui rumus luas segitiga sebarang. Rumus luas segitiga sebarang adalah:a. Rumus Jari-jari Lingkaran Dalam Segitiga
Perhatikan gambar! OP, OQ, dan OR adalah jari-jari lingkaran dalam segitiga. Jika OP = OQ = OR = rd, BC = a, AC = b, dan AB = c, maka:b. Rumus Jari-jari Lingkaran Luar Segitiga
Selanjutnya, perhatikan gambar di bawah ini! Lingkaran yang terbentuk pada gambar adalah lingkaran luar ΔABC yang berpusat di titik O. OA dan OQ adalah jari-jari lingkaran luar. Misalkan OA = OQ = rl, BC = a, AC = b, dan AB = c.Perhatikan ΔAQB dan ΔACP!
Besar ∠ABQ (sudut keliling yang menghadap busur AQ dan menghadap diameter lingkaran) = 90o = ∠APC (karena AP adalah garis tinggi ΔACP, maka AP⊥BC). Besar ∠AQB = ∠ACP karena sudut keliling menghadap busur yang sama). (Materi bahasan sudut keliling akan dibahas pada subbab berikutnya).
Karena terdapat dua buah sudut yang bersesuaian sama besar, maka ΔAQB dan ΔACP sebangun (bentuknya sama, tetapi ukurannya berbeda). Sehingga dapat ditulis secara matematis dalam bentuk berikut.
Sehingga, dapat kita simpulkan untuk sebarang segitiga dengan panjang sisi-sisinya a, b, dan c, serta s = ½ × keliling segitiga, maka jari-jari lingkaran luar segitiga adalah:
Contoh Soal Jari-jari Lingkaran Luar dan Dalam Segitiga
Panjang sisi-sisi sebuah segitiga adalah 6 cm, 8 cm, dan 10 cm. Hitunglah:a. Keliling lingkaran dalam segitiga
b. Luas lingkaran luar segitiga
Penyelesaian:
Diketahui a = 6 cm, b = 8 cm, c = 10 cm
Baca juga: Melukis Lingkaran Luar Segitiga