Sifat-sifat Segitiga (Siku-siku, Sama Kaki, Sama Sisi dan Sembarang)
April 22, 2016
Edit
Berikut ini adalah pembahasan tentang sifat sifat segitiga, yang meliputi sifat sifat segitiga siku siku, sifat sifat segitiga sama kaki, sifat sifat segitiga sembarang, sifat sifat segitiga sama sisi, ciri ciri segitiga sama sisi, ciri ciri segitiga siku siku.
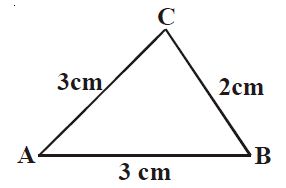
Misalkan diketahui DABC dengan AB = 3 cm, BC = 2 cm, dan AC = 3 cm. Berdasarkan sifat di atas maka berlaku hubungan:
AB + BC > AC <=> 3 + 2 > 3
AB + AC > DC <=> 3 + 3 > 2
AC + BC > AB <=> 3 + 2 > 3
AB - BC = < AB <=> 3 - 2 < 3
AB - AC = < BC <=> 3 - 3 < 2
AC - BC = < AB <=> 3 - 2 < 3
1. Ukur panjang sisi-sisi DABC, yaitu a, b, dan c. Kemudian urutkan hasilnya dari yang terpendek. Urutannya adalah a, b, dan c.
2. Ukur besarnya sudut-sudut DABC, yaitu ÐA, ÐB, dan ÐC. Kemudian urutkan hasilnya mulai dari yang terkecil urutannya adalah ÐA, ÐB, dan ÐC.
Sekarang kamu perhatikan:
ÐA berhadapan dengan sisi a, ÐB berhadapan dengan sisi b dan ÐC berhadapan dengan sisi c. Jadi kesimpulannya adalah:
Untuk mengetahui hubungan antara sudut dalam dengan sudut luar, perhatikan dan simaklah dengan baik uraian di bawah ini.
ÐPQR adalah salah satu sudut dalam DPQR. ÐPQR berpelurus dengan ÐPQT, maka ÐPQT merupakan sudut luar DPQR, demikian juga ÐRSP berpelurus dengan ÐQPR, dan ÐPRU berpelurus dengan ÐPRQ, maka ÐSPR dan ÐPRU juga disebut sudut luar DPQR.
Perhatikanlah kembali Gambar di atas, pada gambar titik S ada di perpanjangan QP sehingga QS adalah garis lurus dan ÐQPR dan ÐSPR paling berpelurus. Hal ini dapat dituliskan
ÐQPR + ÐSPR = 180o <=> ÐSPR = 180o – ÐQPR ... (1)
ÐQPR, ÐPRQ, dan ÐPQR sudut-sudut dalam DPQR, maka
ÐQPR + ÐPQR + ÐPRQ = 180o <=> ÐPRQ + ÐPQR = 180o – ÐQPR ... (2)
Persamaan (1) sama dengan persamaan (2), sehingga ÐSPR = ÐPRQ + ÐPQR.
Dari uraian tersebut dapat disimpulkan bahwa:
Baca juga: Rumus Luas dan Keliling Segitiga
Sifat-Sifat Segitiga
Diantara sifat dari segitiga adalah;a. Ketidaksamaan Sisi Segitiga
Sifat 1
Jumlah panjang dua sisi segitiga lebih dari sisi yang lainnya.
Misalkan diketahui DABC dengan AB = 3 cm, BC = 2 cm, dan AC = 3 cm. Berdasarkan sifat di atas maka berlaku hubungan:
AB + BC > AC <=> 3 + 2 > 3
AB + AC > DC <=> 3 + 3 > 2
AC + BC > AB <=> 3 + 2 > 3
Sifat 2
Selisih panjang dua sisi segitiga kurang dari panjang sisi lainnya.Perhatikan kembali Gambar di atas.
AB - BC = < AB <=> 3 - 2 < 3
AB - AC = < BC <=> 3 - 3 < 2
AC - BC = < AB <=> 3 - 2 < 3
b. Hubungan Sudut dan Segitiga
Untuk mengetahui hubungan sudut dan sisi pada segitiga, perhatikanlah Gambar berikut ini.1. Ukur panjang sisi-sisi DABC, yaitu a, b, dan c. Kemudian urutkan hasilnya dari yang terpendek. Urutannya adalah a, b, dan c.
2. Ukur besarnya sudut-sudut DABC, yaitu ÐA, ÐB, dan ÐC. Kemudian urutkan hasilnya mulai dari yang terkecil urutannya adalah ÐA, ÐB, dan ÐC.
Sekarang kamu perhatikan:
ÐA berhadapan dengan sisi a, ÐB berhadapan dengan sisi b dan ÐC berhadapan dengan sisi c. Jadi kesimpulannya adalah:
Sebuah segitiga, ukuran sudut terkecil berhadapan dengan ukuran sisi terpendek, dan ukuran sudut terbesar berhadapan dengan sisi terpanjang.
c. Hubungan Sudut Dalam dan Sudut Luar Segitiga
Sudut dalam suatu segitiga adalah sudut yang berada di dalam segitiga, sedangkan sudut luar suatu segitiga adalah sudut pelurus dari sudut dalam segitiga tersebut.Untuk mengetahui hubungan antara sudut dalam dengan sudut luar, perhatikan dan simaklah dengan baik uraian di bawah ini.
ÐPQR adalah salah satu sudut dalam DPQR. ÐPQR berpelurus dengan ÐPQT, maka ÐPQT merupakan sudut luar DPQR, demikian juga ÐRSP berpelurus dengan ÐQPR, dan ÐPRU berpelurus dengan ÐPRQ, maka ÐSPR dan ÐPRU juga disebut sudut luar DPQR.
Perhatikanlah kembali Gambar di atas, pada gambar titik S ada di perpanjangan QP sehingga QS adalah garis lurus dan ÐQPR dan ÐSPR paling berpelurus. Hal ini dapat dituliskan
ÐQPR + ÐSPR = 180o <=> ÐSPR = 180o – ÐQPR ... (1)
ÐQPR, ÐPRQ, dan ÐPQR sudut-sudut dalam DPQR, maka
ÐQPR + ÐPQR + ÐPRQ = 180o <=> ÐPRQ + ÐPQR = 180o – ÐQPR ... (2)
Persamaan (1) sama dengan persamaan (2), sehingga ÐSPR = ÐPRQ + ÐPQR.
Dari uraian tersebut dapat disimpulkan bahwa:
Sudut luar dari salah satu sudut dalam segitiga sama dengan jumlah dua sudut dalam yang lainnya.Demikian pembahasan tentang sifat sifat segitiga, sifat sifat segitiga siku siku, sifat sifat segitiga sama kaki, sifat sifat segitiga sembarang, sifat sifat segitiga sama sisi, ciri ciri segitiga sama sisi, ciri ciri segitiga siku siku.
Baca juga: Rumus Luas dan Keliling Segitiga