Sifat-sifat Garis Sejajar
April 11, 2016
Edit
Berikut ini merupakan pembahasan tentang sifat-sifat garis sejajar.
Aksioma: Melalui sebuah titik di luar sebuah garis dapat dilukis tepat satu garis yang sejajar dengan garis tersebut.
Misalkan diketahui garis m dan titik A di luar M. Menurut aksioma di atas, melalui titik A hanya dapat ditarik satu garis lurus yang sejajar dengan garis m. Misalkan garis l.
Bukti: misalkan l // m, maka m juga melalui titik P dengan demikian l // m, maka l juga sejajar k, karena m // k. Hal ini bertentangan dengan sifat satu, berarti pemisahan ini salah, maka l harus memotong. Berarti ketentuan pada sifat satu adalah benar.
Menurut sifat 1, jika k berpotongan dengan m, maka k juga berpotongan dengan l. Hal ini bertentangan dengan ketentuan-ketentuan yang diketahui, yaitu k // l, jadi pemisalan ini salah, seharusnya k // m.
Diketahui 3 buah garis a, b, dan c menurut sifat 2, jika a // b dan b // c, maka a // c.
Demikian pembahasan tentang sifat-sifat dari sebuah garis dapat dikatakan sejajar.
Baca juga: Macam-macam Contoh Garis
Aksioma: Melalui sebuah titik di luar sebuah garis dapat dilukis tepat satu garis yang sejajar dengan garis tersebut.
Misalkan diketahui garis m dan titik A di luar M. Menurut aksioma di atas, melalui titik A hanya dapat ditarik satu garis lurus yang sejajar dengan garis m. Misalkan garis l.
Sifat-sifat Garis Sejajar
Berikut ini adalah sifat-sifat garis sejajar;Sifat 1
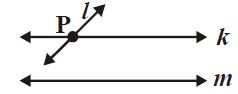
Jika suatu garis memotong salah satu dari dua garis yang sejajar, maka garis itu juga memotong garis lainnya.Misalkan dua buah garis k dan m sejajar, ditulis k // m dan garis l memotong garis k di titik P, maka l juga akan memotong garis m.
Bukti: misalkan l // m, maka m juga melalui titik P dengan demikian l // m, maka l juga sejajar k, karena m // k. Hal ini bertentangan dengan sifat satu, berarti pemisahan ini salah, maka l harus memotong. Berarti ketentuan pada sifat satu adalah benar.
Sifat 2
Jika sebuah garis sejajar dengan 2 buah garis, maka kedua garis itu juga saling sejajar.Misalkan k // l dan l // m, maka k // m, buktikan! Seandainya k tidak sejajar dengan m, maka k harus berpotongan dengan m.
Menurut sifat 1, jika k berpotongan dengan m, maka k juga berpotongan dengan l. Hal ini bertentangan dengan ketentuan-ketentuan yang diketahui, yaitu k // l, jadi pemisalan ini salah, seharusnya k // m.
Diketahui 3 buah garis a, b, dan c menurut sifat 2, jika a // b dan b // c, maka a // c.
Demikian pembahasan tentang sifat-sifat dari sebuah garis dapat dikatakan sejajar.
Baca juga: Macam-macam Contoh Garis