Pengertian Diagonal Bidang dan Diagonal Ruang beserta Rumusnya
Agustus 08, 2016
Edit
Berikut ini adalah pembahasan tentang pengertian diagonal bidang, pengertian diagonal ruang, rumus panjang diagonal bidang, rumus panjang diagonal ruang, contoh soal diagonal bidang, contoh soal diagonal ruang.
Begitupun jika titik A dan titik H dihubungkan, kita akan memperoleh garis AH. Garis seperti EG dan AH inilah yang dinamakan diagonal bidang.
Pada gambar (a), garis EB merupakan diagonal bidang dari kubus ABCD.EFGH. Garis EB terletak pada bidang ABFE dan membagi bidang tersebut menjadi dua buah segitiga siku-siku yaitu segitiga ABE dengan siku-siku di A, dan segitiga BFE dengan siku-siku di F. Perhatikan segitiga ABE pada gambar (b) dengan EB sebagai diagonal bidang.
Berdasarkan teorema Pythagoras, maka:
EB2 = AE2 + AB2
= s2 + s2
= 2s2, sehingga didapat
EB = √2s2 = s√2
Karena semua bidang dalam kubus berbentuk persegi, maka panjang diagonal bidang dari setiap bidang pada kubus nilainya sama. Sehingga dapat kita ambil kesimpulan, jika s merupakan panjang rusuk sebuah kubus, maka berlaku rumus:
Perhatikan segitiga pada gambar (d) dengan TQ sebagai diagonal bidang PQUT, PQ = p, dan TP = t. Berdasarkan teorema Pythagoras, maka:
TQ2 = PQ2 + TP2
= p2 + t2
TQ = √p2 + t2
Amati kembali gambar (c). Tentukan panjang diagonal bidang yang lainnya!
Perhatikan kubus RSTU.VWXY di bawah ini!
Dengan menggunakan teorema Pythagoras, tentukanlah panjang di ago nal ruang TV, SY, RX, dan UW! Diskusikan hasilnya dengan teman sebangkumu, kemudian bandingkanlah hasilnya dengan kesimpulan di bawah ini!
Jika s = panjang rusuk sebuah kubus, maka berlaku rumus:
Pada gambar di atas, PV dan SU merupakan diagonal ruang balok PQRS.TUVW. Jika kamu perhatikan, apakah diagonal PV lebih panjang jika dibandingkan dengan diagonal SU?
Perhatikan penjelasan berikut ini.
Karena segitiga PRV merupakan segitiga siku-siku dengan siku-siku di R, maka berlaku teorema Pythagoras, sehingga diperoleh PV2 = PR2 + VR2, dimana PR sebagai diagonal bidang PQRS.
Berdasarkan uraian di atas, kita peroleh hubungan:
PV2 = (PQ2 + QR2 + VR2)
= p2 + l2 + t2
PV = √p2 + l2 + t2……………………………. (1)
Karena segitiga QSU merupakan segitiga siku-siku dengan siku-siku di Q, maka berlaku teorema Pythagoras, sehingga diperoleh SU2 = QS2 + QU2, dimana QS sebagai diagonal bidang PQRS.
Berdasarkan uraian di atas, kita peroleh hubungan:
SU2 = (PQ2 + PS2 + QU2)
= p2 + l2 + t2
SU = √p2 + l2 + t2………………………….... (2)
Dari persamaan (1) dan (2), diperoleh bahwa PV = SU.
Sehingga jika sebuah balok mempunyai ukuran panjang p, lebar l, dan tinggi t, maka berlaku rumus:
Penyelesaian:
rusuk = s = 16 cm
Panjang diagonal bidang = s√2 = 16√2 cm
Panjang diagonal ruang = s√3 = 16√3 cm
2. Perhatikan balok PQRS.TUVW di bawah ini! Diketahui PQ = 23 cm, QR = 13 cm, dan VR = 7 cm. Hitunglah panjang diagonal bidang UQRV dan panjang diagonal ruang balok tersebut!
Penyelesaian:
PQ = p = 23 cm,
QR = l = 13 cm, dan
VR = t = 7 cm
Panjang diagonal bidang UQRV = √QR2 + VR2
= √l2 + t2
= √132 + 72
= √169 + 49
= √218 cm
Panjang diagonal ruang =√p2 + l2 + t2
=√232 + 132 + 72
= √529 + 169 + 497
= √747
= 3√83 cm
Baca juga: Unsur-unsur Kubus dan Balok
Pengertian Diagonal Bidang dan Diagonal Ruang
Perhatikan gambar berikut! Jika titik E dan titik G dihubungkan, maka akan diperoleh garis EG.Begitupun jika titik A dan titik H dihubungkan, kita akan memperoleh garis AH. Garis seperti EG dan AH inilah yang dinamakan diagonal bidang.
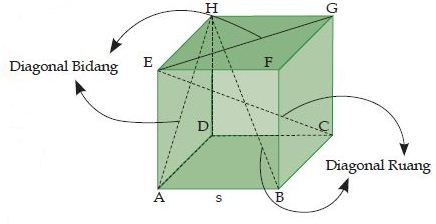 |
| Gambar: Diagonal Bidang dan Diagonal Ruang |
Jadi, Diagonal Bidang yaitu garis yang menghubungkan dua buah titik sudut yang saling berhadapan dalam satu bidang.Perhatikan kembali gambar di atas! Jika titik E dan titik C dihubungkan kita akan memperoleh garis EC, begitu juga jika titik H dan titik B kita hubungkan akan diperoleh garis HB. Garis seperti EC dan HB inilah yang dinamakan dengan diagonal ruang.
Jadi, diagonal ruang adalah garis yang menghubungkan dua buah titik sudut yang saling berhadapan tak sebidang.
Rumus Panjang Diagonal Bidang
Selanjutnya perhatikan gambar berikut!Pada gambar (a), garis EB merupakan diagonal bidang dari kubus ABCD.EFGH. Garis EB terletak pada bidang ABFE dan membagi bidang tersebut menjadi dua buah segitiga siku-siku yaitu segitiga ABE dengan siku-siku di A, dan segitiga BFE dengan siku-siku di F. Perhatikan segitiga ABE pada gambar (b) dengan EB sebagai diagonal bidang.
Berdasarkan teorema Pythagoras, maka:
EB2 = AE2 + AB2
= s2 + s2
= 2s2, sehingga didapat
EB = √2s2 = s√2
Karena semua bidang dalam kubus berbentuk persegi, maka panjang diagonal bidang dari setiap bidang pada kubus nilainya sama. Sehingga dapat kita ambil kesimpulan, jika s merupakan panjang rusuk sebuah kubus, maka berlaku rumus:
Panjang diagonal bidang kubus = s√2Sekarang perhatikan gambar (c). Pada bidang PQUT, terdapat diagonal bidang TQ, dan TQ membagi bidang PQUT menjadi dua buah segitiga siku-siku yaitu segitiga PTQ dengan siku-siku di P dan segitiga QUT dengan siku-siku di U.
Perhatikan segitiga pada gambar (d) dengan TQ sebagai diagonal bidang PQUT, PQ = p, dan TP = t. Berdasarkan teorema Pythagoras, maka:
TQ2 = PQ2 + TP2
= p2 + t2
TQ = √p2 + t2
Amati kembali gambar (c). Tentukan panjang diagonal bidang yang lainnya!
Rumus Panjang Diagonal Ruang
Untuk menentukan panjang diagonal ruang kubus, lakukanlah kegiatan berikut ini!Perhatikan kubus RSTU.VWXY di bawah ini!
Dengan menggunakan teorema Pythagoras, tentukanlah panjang di ago nal ruang TV, SY, RX, dan UW! Diskusikan hasilnya dengan teman sebangkumu, kemudian bandingkanlah hasilnya dengan kesimpulan di bawah ini!
Jika s = panjang rusuk sebuah kubus, maka berlaku rumus:
Panjang diagonal ruang kubus = s√3Sedangkan untuk menentukan panjang diagonal ruang balok, perhatikan gambar berikut ini!
Pada gambar di atas, PV dan SU merupakan diagonal ruang balok PQRS.TUVW. Jika kamu perhatikan, apakah diagonal PV lebih panjang jika dibandingkan dengan diagonal SU?
Perhatikan penjelasan berikut ini.
Karena segitiga PRV merupakan segitiga siku-siku dengan siku-siku di R, maka berlaku teorema Pythagoras, sehingga diperoleh PV2 = PR2 + VR2, dimana PR sebagai diagonal bidang PQRS.
Berdasarkan uraian di atas, kita peroleh hubungan:
PV2 = (PQ2 + QR2 + VR2)
= p2 + l2 + t2
PV = √p2 + l2 + t2……………………………. (1)
Karena segitiga QSU merupakan segitiga siku-siku dengan siku-siku di Q, maka berlaku teorema Pythagoras, sehingga diperoleh SU2 = QS2 + QU2, dimana QS sebagai diagonal bidang PQRS.
Berdasarkan uraian di atas, kita peroleh hubungan:
SU2 = (PQ2 + PS2 + QU2)
= p2 + l2 + t2
SU = √p2 + l2 + t2………………………….... (2)
Dari persamaan (1) dan (2), diperoleh bahwa PV = SU.
Sehingga jika sebuah balok mempunyai ukuran panjang p, lebar l, dan tinggi t, maka berlaku rumus:
Panjang diagonal ruang balok = √p2 + l2 + t2
Contoh Soal
1. Sebuah kubus mempunyai panjang rusuk 16 cm. Hitunglah panjang diagonal bidang dan panjang diagonal ruang kubus tersebut!Penyelesaian:
rusuk = s = 16 cm
Panjang diagonal bidang = s√2 = 16√2 cm
Panjang diagonal ruang = s√3 = 16√3 cm
2. Perhatikan balok PQRS.TUVW di bawah ini! Diketahui PQ = 23 cm, QR = 13 cm, dan VR = 7 cm. Hitunglah panjang diagonal bidang UQRV dan panjang diagonal ruang balok tersebut!
Penyelesaian:
PQ = p = 23 cm,
QR = l = 13 cm, dan
VR = t = 7 cm
Panjang diagonal bidang UQRV = √QR2 + VR2
= √l2 + t2
= √132 + 72
= √169 + 49
= √218 cm
Panjang diagonal ruang =√p2 + l2 + t2
=√232 + 132 + 72
= √529 + 169 + 497
= √747
= 3√83 cm
Baca juga: Unsur-unsur Kubus dan Balok




