Pengertian dan Contoh Soal Persamaan Linear Dua Variabel (PLDV)
Mei 31, 2016
Edit
Berikut ini merupakan pembahasan tentang Persamaan Linear Dua Variabel, sistem persamaan linear dua variabel, persamaan linier dua variabel, sistem persamaan linier dua variabel, persamaan linear 2 variabel, pengertian persamaan linear dua variabel, contoh soal persamaan linear dua variabel, pldv, contoh soal persamaan linier dua variabel.
Ibu Hayati dan ibu Sofi pergi berbelanja di pasar. Ibu Hayati membeli 3 kg apel dan 4 kg jeruk dengan harga Rp 58.000,00. Ibu Sofi membeli 4 kg apel dan 3 kg jeruk dengan harga Rp 61.000,00.
Dapatkah kamu menentukan harga 2 kg apel dan 3 kg jeruk? Persoalan tersebut dapat diselesaikan dengan persamaan liner. Caranya dengan memisalkan buah apel sebagai x dan buah jeruk sebagai y lalu memasukkannya dalam sebuah persamaan.
Persamaan-persaman di atas memiliki sebuah variabel, yaitu x, y, dan z. Lalu bagaimana bentuk persamaan linear dua variabel? Ayo kita simak pada uraian berikut!
Himpunan penyelesaian dari persamaan ax + by = c merupakan pasangan berurutan (x, y). Hal ini pernah kalian pelajari juga pada pembahasan yang membahas tentang fungsi.
Agar lebih mudah mencari penyelesaian suatu persamaan biasanya digunakan tabel. Perhatikan contoh berikut ini!
a. x dan y variabel pada himpunan bilangan cacah
b. x dan y variabel pada himpunan bilangan real
Penyelesaian:
a. Perhatikan x dan y variabel pada himpunan bilangan cacah, jika dihasilkan nilai yang bukan bilangan cacah maka itu bukan himpunan penyelesaiannya.
Jadi, himpunan penyelesaiannya adalah: {(0, 4), (1, 2), (2, 0)}
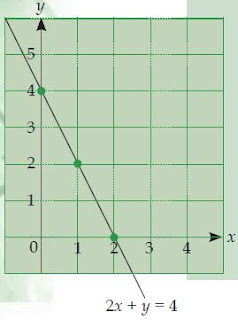
b. Jika x dan y variabel pada himpunan bilangan real, maka terdapat tak hingga banyaknya himpunan penyelesaiannya. Jika digambarkan dalam grafik maka diperoleh garis lurus seperti terlihat pada gambar di bawah ini.
Himpunan penyelesaiannya dapat ditulis: {(x, y)|2x + y = 4; x, y ∈ R }
Baca juga: Soal Cerita Sistem Persamaan Linear
Ibu Hayati dan ibu Sofi pergi berbelanja di pasar. Ibu Hayati membeli 3 kg apel dan 4 kg jeruk dengan harga Rp 58.000,00. Ibu Sofi membeli 4 kg apel dan 3 kg jeruk dengan harga Rp 61.000,00.
Dapatkah kamu menentukan harga 2 kg apel dan 3 kg jeruk? Persoalan tersebut dapat diselesaikan dengan persamaan liner. Caranya dengan memisalkan buah apel sebagai x dan buah jeruk sebagai y lalu memasukkannya dalam sebuah persamaan.
Persamaan Linear Dua Variabel
Masih ingat apa yang dimaksud dengan persamaan linear satu variabel? Coba kalian perhatikan persamaan berikut.- 2x + 3 = –4;
- 3y – 2 = 5; dan
- –z + 3 = 7.
Persamaan-persaman di atas memiliki sebuah variabel, yaitu x, y, dan z. Lalu bagaimana bentuk persamaan linear dua variabel? Ayo kita simak pada uraian berikut!
Pengertian Persamaan Linear Dua Variabel
Misalkan kita menemukan persamaan 2x + 3y = 6 atau q – 2r = 3. Pada persamaan tersebut masing-masing mempunyai dua variabel, yaitu x dan y serta q dan r.Jadi, persamaan linear dua variabel adalah persamaan yang dapat dituliskan dalam bentuk ax + by = c dimana x dan y adalah variabel dan a, b, c ∈ R (a ≠ 0, b ≠ 0).
Contoh Persamaan Linear Dua Variabel
- 3x – 2y = 10 (persamaan linear dua variabel)
- –4p – 2q = 3 (persamaan linear dua variabel)
- x2 – 2y = 5 (bukan persamaan linear dua variabel)
- 3x – 2y + 5z = 10 (bukan persamaan linear dua variabel)
Penyelesaian Persamaan Linear Dua Variabel
Menentukan penyelesaian persamaan linear dua variabel berbentuk ax + by = c sama artinya dengan mencari bilangan-bilangan pengganti x dan y yang memenuhi persamaan tersebut.Himpunan penyelesaian dari persamaan ax + by = c merupakan pasangan berurutan (x, y). Hal ini pernah kalian pelajari juga pada pembahasan yang membahas tentang fungsi.
Agar lebih mudah mencari penyelesaian suatu persamaan biasanya digunakan tabel. Perhatikan contoh berikut ini!
Contoh Soal Persamaan Linear Dua Variable
Tentukan himpunan penyelesaian dari PLDV dari 2x + y = 4, jika:a. x dan y variabel pada himpunan bilangan cacah
b. x dan y variabel pada himpunan bilangan real
Penyelesaian:
a. Perhatikan x dan y variabel pada himpunan bilangan cacah, jika dihasilkan nilai yang bukan bilangan cacah maka itu bukan himpunan penyelesaiannya.
Jadi, himpunan penyelesaiannya adalah: {(0, 4), (1, 2), (2, 0)}
b. Jika x dan y variabel pada himpunan bilangan real, maka terdapat tak hingga banyaknya himpunan penyelesaiannya. Jika digambarkan dalam grafik maka diperoleh garis lurus seperti terlihat pada gambar di bawah ini.
Himpunan penyelesaiannya dapat ditulis: {(x, y)|2x + y = 4; x, y ∈ R }
Baca juga: Soal Cerita Sistem Persamaan Linear