Sifat-sifat Penjumlahan pada Bilangan Bulat
Februari 13, 2016
Edit
Pembahasan berikut ini adalah sebagai pelengkap dari materi operasi hitung pada bilangan bulat, yaitu tentang sifat-sifat penjumlahan bilangan bulat baik positif maupun negatif yang mencakup di dalamnya tentang sifat-sifat bilangan bulat.
a. 2 + 9 = 1 ® 2 dan 9 adalah bilangan bulat.
Hasil penjumlahannya 11, juga bilangan bulat.
b. (–11) + (–9) = –20 ® –11 dan –9 adalah bilangan bulat
Hasil penjumlahannya –20, juga bilangan bulat.
c. –12 + 25 = 13 ® –12 dan 25 adalah bilangan bulat.
Hasil penjumlahannya 13, juga bilangan bulat.
Berdasarkan contoh-contoh di atas dapat disimpulkan bahwa penjumlahan dua buah bilangan bulat atau lebih akan selalu menghasilkan bilangan bulat juga.
a. 5 + 7 = 12
7 + 5 = 12
Jadi, 5 + 7 = 7 + 5
b. 10 + (–5) = 5
(–5) + 10 = 5
Jadi, 10 + (–5) = (–5) + 10
c. –4 + (–5) = –9
(–5) + (–4) = –9
Jadi, –4 + (–5) = –5 + (–4)
Dari contoh-contoh di atas dapat disimpulkan bahwa
a. (–5 + 7) + 8 = 2 + 8 = 10
–5 + (7 + 8) = –5 + 15 = 10
Jadi, (–5 + 7) + 8 = –5 + (7 + 8)
b. {7 + (–2)} + 6 = 5 + 6 = 11
7 + {(–2) + 6} = 7 + 4 = 11
Jadi, {7 + (–2)} + 6 = 7 + {(–2) + 6}
c. {–3 + (–6)} + (–5) = –9 + (–5) = –14
–3 + {(–6)} + (–5) = –3 + {(–6) + (–5)}
Jadi, {–3 + –6)} + (–5) = –3 + {(–6) + (–5)}
Berdasarkan contoh-contoh di atas dapat disimpulkan bahwa
a. 2 + 0 = 2 c. –10 + 0 = –10
b. 5 + 0 = 5 d. 0 + 2 = 2
Dari contoh-contoh di atas dapat disimpulkan bahwa penjumlahan suatu bilangan dengan nol atau sebaliknya akan menghasilkan bilangan itu sendiri. Nol disebut unsur identitas penjumlahan.
Contoh:
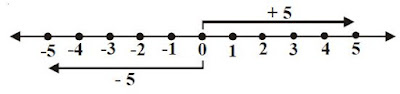
Tulislah lawan dari 5.
Penyelesaian:
Kita cari bilangan lain yang berjarak sama dari 0, tetapi arahnya berlawanan dengan 5. Bilangan itu adalah –5. Jadi, invers (lawan) dari 5 adalah –5.
Secara umum dituliskan:
Baca juga: Daftar simbol dalam matematika
Macam-macam Sifat Penjumlahn Bilangan Bulat
1. Sifat tertutup
Perhatikan contoh di bawah ini:a. 2 + 9 = 1 ® 2 dan 9 adalah bilangan bulat.
Hasil penjumlahannya 11, juga bilangan bulat.
b. (–11) + (–9) = –20 ® –11 dan –9 adalah bilangan bulat
Hasil penjumlahannya –20, juga bilangan bulat.
c. –12 + 25 = 13 ® –12 dan 25 adalah bilangan bulat.
Hasil penjumlahannya 13, juga bilangan bulat.
Berdasarkan contoh-contoh di atas dapat disimpulkan bahwa penjumlahan dua buah bilangan bulat atau lebih akan selalu menghasilkan bilangan bulat juga.
Untuk setiap bilangan bulat a dan b, jika a + b = c, maka c juga bilangan bulat.Sifat ini disebut tertutup terhadap penjumlahan bilangan bulat.
2. Sifat komutatif (pertukaran)
Perhatikan beberapa contoh berikut:a. 5 + 7 = 12
7 + 5 = 12
Jadi, 5 + 7 = 7 + 5
b. 10 + (–5) = 5
(–5) + 10 = 5
Jadi, 10 + (–5) = (–5) + 10
c. –4 + (–5) = –9
(–5) + (–4) = –9
Jadi, –4 + (–5) = –5 + (–4)
Dari contoh-contoh di atas dapat disimpulkan bahwa
Untuk setiap bilangan bulat a dan b, selalu berlaku a + b = b + a.Sifat ini disebut komutatif (pertukaran) terhadap penjumlahan bilangan bulat.
 |
| Sifat-sifat Penjumlahan |
3. Sifat asosiatif (pengelompokan) terhadap penjumlahan bilangan bulat.
Perhatikan contoh-contoh berikut ini:a. (–5 + 7) + 8 = 2 + 8 = 10
–5 + (7 + 8) = –5 + 15 = 10
Jadi, (–5 + 7) + 8 = –5 + (7 + 8)
b. {7 + (–2)} + 6 = 5 + 6 = 11
7 + {(–2) + 6} = 7 + 4 = 11
Jadi, {7 + (–2)} + 6 = 7 + {(–2) + 6}
c. {–3 + (–6)} + (–5) = –9 + (–5) = –14
–3 + {(–6)} + (–5) = –3 + {(–6) + (–5)}
Jadi, {–3 + –6)} + (–5) = –3 + {(–6) + (–5)}
Berdasarkan contoh-contoh di atas dapat disimpulkan bahwa
Untuk setiap bilangan bulat a, b, dan c selalu berlaku (a + b) + c = a + (b + c).Sifat ini disebut asosiatif terhadap penjumlahan bilangan bulat.
4. Unsur identitas penjumlahan
Perhatikan contoh-contoh berikut:a. 2 + 0 = 2 c. –10 + 0 = –10
b. 5 + 0 = 5 d. 0 + 2 = 2
Dari contoh-contoh di atas dapat disimpulkan bahwa penjumlahan suatu bilangan dengan nol atau sebaliknya akan menghasilkan bilangan itu sendiri. Nol disebut unsur identitas penjumlahan.
Untuk sebarang bilangan bulat a, selalu berlaku a + 0 = 0 + a = a.
5. Invers/lawan
Setiap bilangan bulat mempunyai invers atau lawan. Lawan dari suatu bulangan bulat adalah bilangan bulat lain yang letaknya pada garis bilangan berjarak sama dari titik nol, tetapi arahnya berlawanan dengan bilangan bulat semula.Contoh:
Tulislah lawan dari 5.
Penyelesaian:
Kita cari bilangan lain yang berjarak sama dari 0, tetapi arahnya berlawanan dengan 5. Bilangan itu adalah –5. Jadi, invers (lawan) dari 5 adalah –5.
Secara umum dituliskan:
Lawan (invers) dari a adalah –a.Demikian pembahasan lengkap tentang sifat-sifat penjumlahan pada bilangan bulat dilengkapi dengan contohnya masing-masing.
Baca juga: Daftar simbol dalam matematika