150 Daftar Bilangan Triple Pythagoras dan 4 Tipe Khusus
Mei 09, 2015
Edit
Pada pembahasan tentang rumus teorema pythagoras telah disinggung tentang segita yang mempunyai sisi-sisi yang panjangnya tertentu sehingga pasti membentuk segitiga siku-siku.
Sisi-sisi tersebut disebut sebagai triple pythagoras. Jadi, apa yang dimaksud dengan triple pythagoras?
Susunan bilangan triple pythagoras dapat dilihat pada tabel berikut ini!
0. (a, b, c)
1. (3,4,5)
2. (5,12,13)
3. (7,24,25)
4. (8,15,17)
5. (9,40,41)
6. (11,60,61)
7. (12,35,37)
8. (13,84,85)
9. (15,112,113)
10. (16,63,65)
11. (17,144,145)
12. (19,180,181)
13. (20,21,29)
14. (20,99,101)
15. (21,220,221)
16. (23,264,265)
17. (24,143,145)
18. (25,312,313)
19. (27,364,365)
20. (28,45,53)
21. (28,195,197)
22. (29,420,421)
23. (31,480,481)
24. (32,255,257)
25. (33,56,65)
26. (33,544,545)
27. (35,612,613)
28. (36,77,85)
29. (36,323,325)
30. (37,684,685)
31. (39,80,89)
32. (39,760,761)
33. (40,399,401)
34. (41,840,841)
35. (43,924,925)
36. (44,117,125)
37. (44,483,485)
38. (48,55,73)
39. (48,575,577)
40. (51,140,149)
41. (52,165,173)
42. (52,675,677)
43. (56,783,785)
44. (57,176,185)
45. (60,91,109)
46. (60,221,229)
47. (60,899,901)
48. (65,72,97)
49. (68,285,293)
50. (69,260,269)
51. (75,308,317)
52. (76,357,365)
53. (84,187,205)
54. (84,437,445)
55. (85,132,157)
56. (87,416,425)
57. (88,105,137)
58. (92,525,533)
59. (93,476,485)
60. (95,168,193)
61. (96,247,265)
62. (100,621,629)
63. (104,153,185)
64. (105,208,233)
65. (105,608,617)
66. (108,725,733)
67. (111,680,689)
68. (115,252,277)
69. (116,837,845)
70. (119,120,169)
71. (120,209,241)
72. (120,391,409)
73. (123,836,845)
74. (124,957,965)
75. (129,920,929)
76. (132,475,493)
77. (133,156,205)
78. (135,352,377)
79. (136,273,305)
80. (140,171,221)
81. (145,408,433)
82. (152,345,377)
83. (155,468,493)
84. (156,667,685)
85. (160,231,281)
86. (161,240,289)
87. (165,532,557)
88. (168,425,457)
89. (168,775,793)
90. (175,288,337)
91. (180,299,349)
92. (184,513,545)
93. (185,672,697)
94. (189,340,389)
95. (195,748,773)
96. (200,609,641)
97. (203,396,445)
98. (204,253,325)
99. (205,828,853)
100. (207,224,305)
101. (215,912,937)
102. (216,713,745)
103. (217,456,505)
104. (220,459,509)
105. (225,272,353)
106. (228,325,397)
107. (231,520,569)
108. (232,825,857)
109. (240,551,601)
110. (248,945,977)
111. (252,275,373)
112. (259,660,709)
113. (260,651,701)
114. (261,380,461)
115. (273,736,785)
116. (276,493,565)
117. (279,440,521)
118. (280,351,449)
119. (280,759,809)
120. (287,816,865)
121. (297,304,425)
122. (300,589,661)
123. (301,900,949)
124. (308,435,533)
125. (315,572,653)
126. (319,360,481)
127. (333,644,725)
128. (336,377,505)
129. (336,527,625)
130. (341,420,541)
131. (348,805,877)
132. (364,627,725)
133. (368,465,593)
134. (369,800,881)
135. (372,925,997)
136. (385,552,673)
137. (387,884,965)
138. (396,403,565)
139. (400,561,689)
140. (407,624,745)
141. (420,851,949)
142. (429,460,629)
143. (429,700,821)
144. (432,665,793)
145. (451,780,901)
146. (455,528,697)
147. (464,777,905)
148. (468,595,757)
149. (473,864,985)
150. (481,600,769)
151. (504,703,865)
152. (533,756,925)
153. (540,629,829)
154. (555,572,797)
155. (580,741,941)
156. (615,728,953)
157. (616,663,905)
158. (696,697,985)
Demikian pembahasan tentang bilangan-bilangan triple pythagoras yang membentuk segitiga siku-siku menurut rumus teorema pythagoras.
Baca juga: Pembuktian Teorema Pythagoras
Sisi-sisi tersebut disebut sebagai triple pythagoras. Jadi, apa yang dimaksud dengan triple pythagoras?
Pengertian triple pythagoras
Apakah yang dimaksud dengan tripel pythagoras?
Triple pythagoras adalah adalah 3 (tiga) bilangan asli yang memenuhi rumus teorema pythagoras. Rumus teorema pythagoras yaitu c2 = a2 + b2.Baca juga: Pembuktian Teorema Pythagoras
Macam-macam Tipe Triple Pythagoras
Triple pythagoras ini masih mempunyai 4 bilangan yang susunan bilangannya teratur dan membentuk pola tertentu atau sering disebut sebagai 4 tipe triple pythagoras.Susunan bilangan triple pythagoras dapat dilihat pada tabel berikut ini!
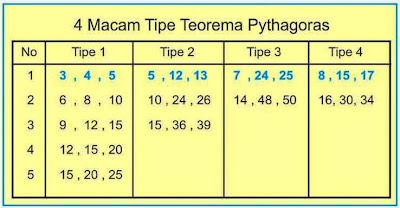 |
| Gambar: 4 macam tipe triple pythagoras |
158 daftar bilangan triple pythagoras pembentuk segitiga siku-siku
Adapaun daftar bilangan triple pythagoras yang membentuk segitiga siku-siku berdasarkan rumus teorema pythagoras adalah sebagai berikut:0. (a, b, c)
1. (3,4,5)
2. (5,12,13)
3. (7,24,25)
4. (8,15,17)
5. (9,40,41)
6. (11,60,61)
7. (12,35,37)
8. (13,84,85)
9. (15,112,113)
10. (16,63,65)
11. (17,144,145)
12. (19,180,181)
13. (20,21,29)
14. (20,99,101)
15. (21,220,221)
16. (23,264,265)
17. (24,143,145)
18. (25,312,313)
19. (27,364,365)
20. (28,45,53)
21. (28,195,197)
22. (29,420,421)
23. (31,480,481)
24. (32,255,257)
25. (33,56,65)
26. (33,544,545)
27. (35,612,613)
28. (36,77,85)
29. (36,323,325)
30. (37,684,685)
31. (39,80,89)
32. (39,760,761)
33. (40,399,401)
34. (41,840,841)
35. (43,924,925)
36. (44,117,125)
37. (44,483,485)
38. (48,55,73)
39. (48,575,577)
40. (51,140,149)
41. (52,165,173)
42. (52,675,677)
43. (56,783,785)
44. (57,176,185)
45. (60,91,109)
46. (60,221,229)
47. (60,899,901)
48. (65,72,97)
49. (68,285,293)
50. (69,260,269)
51. (75,308,317)
52. (76,357,365)
53. (84,187,205)
54. (84,437,445)
55. (85,132,157)
56. (87,416,425)
57. (88,105,137)
58. (92,525,533)
59. (93,476,485)
60. (95,168,193)
61. (96,247,265)
62. (100,621,629)
63. (104,153,185)
64. (105,208,233)
65. (105,608,617)
66. (108,725,733)
67. (111,680,689)
68. (115,252,277)
69. (116,837,845)
70. (119,120,169)
71. (120,209,241)
72. (120,391,409)
73. (123,836,845)
74. (124,957,965)
75. (129,920,929)
76. (132,475,493)
77. (133,156,205)
78. (135,352,377)
79. (136,273,305)
80. (140,171,221)
81. (145,408,433)
82. (152,345,377)
83. (155,468,493)
84. (156,667,685)
85. (160,231,281)
86. (161,240,289)
87. (165,532,557)
88. (168,425,457)
89. (168,775,793)
90. (175,288,337)
91. (180,299,349)
92. (184,513,545)
93. (185,672,697)
94. (189,340,389)
95. (195,748,773)
96. (200,609,641)
97. (203,396,445)
98. (204,253,325)
99. (205,828,853)
100. (207,224,305)
101. (215,912,937)
102. (216,713,745)
103. (217,456,505)
104. (220,459,509)
105. (225,272,353)
106. (228,325,397)
107. (231,520,569)
108. (232,825,857)
109. (240,551,601)
110. (248,945,977)
111. (252,275,373)
112. (259,660,709)
113. (260,651,701)
114. (261,380,461)
115. (273,736,785)
116. (276,493,565)
117. (279,440,521)
118. (280,351,449)
119. (280,759,809)
120. (287,816,865)
121. (297,304,425)
122. (300,589,661)
123. (301,900,949)
124. (308,435,533)
125. (315,572,653)
126. (319,360,481)
127. (333,644,725)
128. (336,377,505)
129. (336,527,625)
130. (341,420,541)
131. (348,805,877)
132. (364,627,725)
133. (368,465,593)
134. (369,800,881)
135. (372,925,997)
136. (385,552,673)
137. (387,884,965)
138. (396,403,565)
139. (400,561,689)
140. (407,624,745)
141. (420,851,949)
142. (429,460,629)
143. (429,700,821)
144. (432,665,793)
145. (451,780,901)
146. (455,528,697)
147. (464,777,905)
148. (468,595,757)
149. (473,864,985)
150. (481,600,769)
151. (504,703,865)
152. (533,756,925)
153. (540,629,829)
154. (555,572,797)
155. (580,741,941)
156. (615,728,953)
157. (616,663,905)
158. (696,697,985)
Demikian pembahasan tentang bilangan-bilangan triple pythagoras yang membentuk segitiga siku-siku menurut rumus teorema pythagoras.
Baca juga: Pembuktian Teorema Pythagoras
